A local diabatisation method for two-state adiabatic conical intersections
The topography around a conical intersection (CI) regulates the non-adiabatic transitions, thereby governing the deactivation pathway, products and lifetime of non-radiative decay processes.[1-3] Hence, a detailed depiction of a CI provides valuable information on a molecule's photodeactivation. A new methodology to characterise CIs between two adiabatic electronic states will be presented, from which the non-adiabatic coupling vectors (NACs) can be calculated in a wave function-free, energy-based approach.[4] The branching space coordinates are identified only based on the state’s Hessians and gradients at the CI geometry. NAC terms are constructed after converting the adiabatic potential energy surface (PES) to a diabatic representation by fitting the PES around the CI in the branching space, as shown in Figure 1.
To prove the universality of the developed methodology, the minimum-energy CI (MECI) between the first (S1) and second (S2) singlet excited states of formamide is investigated at the state-averaged complete active space self-consistent field (SA-CASSCF) and extended multi-state complete active space second-order perturbation theory (XMS-CASPT2) levels of theory. In addition, the asymmetrical MECI between the ground state (S0) and S1 of cyclopropanone is evaluated using SA-CASSCF, as well as (ME)CIs between the S1 and S2 states of benzene using SA-CASSCF and time-dependent density functional theory (TDDFT). Finally, a CI between the S1 and S2 excited states of thiophene was analysed using TDDFT. The evolution of the states' characters, and projection of the NACs and gradients on the branching plane computed ab-initio and composed from the developed methodology are analogue for all electronic structure methods and software programmes used.
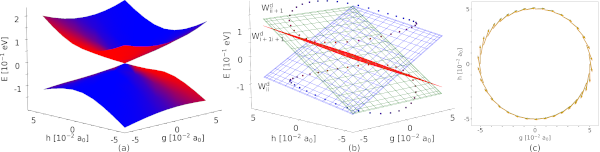
Figure 1: SA-CASSCF(8,7) PES around the S0-S1 asymmetrical MECI of cyclopropanone along the branching space coordinates (a) and diabatic approximation of this PES with circumferences of the adiabatic energy cones (b) coloured according to the state characters. Projection of the NAC vectors calculated using SA-CASSCF(8,7) (green) and composed from our methodology (orange) on the branching space coordinates in the vicinity of cyclopropanone’s S0-S1 asymmetrical MECI (c).
[2] Lluis Blancafort, ChemPhysChem, 2014, 15(15), 3166-3181.
[3] Spiridoula Matsika, Chemical Reviews, 2021, 121(15), 9407-9449.
[4] Eva Vandaele, Momir Malis, Sandra Luber, Manuscript submitted for publication.